科研进展丨本实验室阴帅组与中科院物理所李自翔组合作在量子临界动力学研究中取得新进展

      近日，中山大学物理学院、广东省磁电物性分析与器件重点实验室阴帅副教授团队与中国科学院物理研究所李自翔特聘研究员团队合作在量子临界动力学领域取得重要突破。他们的研究成果“狄拉克系统中超越 Kibble-Zurek 前提条件的有限时间标度”(Finite-time scaling beyond the Kibble-Zurek prerequisite in Dirac systems) 发表于国际重要期刊《自然・通讯》（Nature Communications）。该论文首次揭示强相互作用狄拉克费米子系统临界点的非平衡动力学，将著名的 Kibble-Zurek 机制和有限时间标度理论扩展到包含初态有无能隙激发的系统中，为理解非平衡量子临界现象提供了全新视角。

      探索临界点附近的非平衡普适性质是统计物理和凝聚态物理的核心课题之一。在上世纪七十年代，T. W. B. Kibble 在宇宙学研究中提出了描述拓扑缺陷形成的驱动动力学机制，后由W. H. Zurek 推广到凝聚态系统的驱动临界动力学中，形成了著名的 Kibble-Zurek 机制。钟凡教授等首先发现临界点附近驱动过程的完整标度，进而提出有限时间标度（Finite-time scaling, FTS）理论，不仅系统地刻画整个驱动过程动力学标度性质，还推广到包含不同初态、多种驱动方式的情形，并发展了一系列确定系统临界性质的非平衡方法。

      然而，传统Kibble-Zurek 机制基于绝热-脉冲假设(Adibatic-impulse scenario)，其有一个重要前提，即要求驱动初始阶段系统处于有能隙的态，以保证初始阶段的绝热性。但在狄拉克费米子临界点中，初始态可以设置为无能隙的狄拉克半金属态（如图1）。这类系统的临界动力学是否仍遵循Kibble-Zurek 机制和有限时间标度？传统理论无法回答。

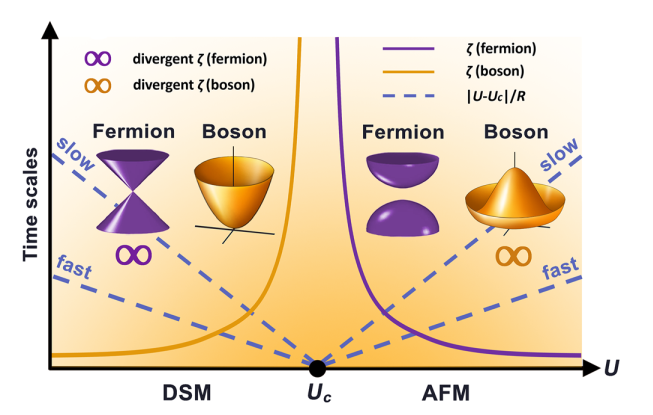
图1 狄拉克临界点驱动动力学时间尺度示意图

      对此，本研究团队聚焦二维强相互作用狄拉克系统，首次通过行列式量子蒙特卡洛（DQMC）方法，对两类典型狄拉克费米子系统的临界动力学模型进行了系统研究。研究发现，即使系统从无隙的狄拉克半金属相开始演化，违反传统Kibble-Zurek 机制的 “有能隙初态” 前提，其驱动临界动力学仍然可以用有限时间标度标度形式描述。通过深入分析，团队提出了一个普适判据：即当无能隙相的动态临界指数z’和量子临界点的驱动速率的标度维度r满足

z’<r

时，Kibble-Zurek 机制和有限时间标度理论仍能有效适用。

      团队进而利用有限时间标度形式，高效获取了可靠的临界指数。和传统平衡态方法中需依赖大尺寸和复杂修正相比，该研究通过调控驱动速率可以有效抑制有限尺寸效应，为费米子系统临界性质的数值研究提供了新的方案。

      中山大学物理学院本科生曾植（现英国帝国理工学院研究生）、余荫铠（现中国科学院物理所研究生）、研究生黎智轩为论文的共同第一作者，中国科学院物理研究所的李自翔特聘研究员和中山大学广东省磁电物性分析与器件重点实验室成员、中山大学物理学院阴帅副教授为论文共同通讯作者。本项目得到了国家自然科学基金、广东省和广州市科技计划项目等资金支持。

原文链接：https://www.nature.com/articles/s41467-025-61611-6